位相問題
結晶内の電子密度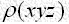 は構造因子
は構造因子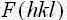 を係数とする次のような三次元フーリエ級数で表すことが出来ます。
を係数とする次のような三次元フーリエ級数で表すことが出来ます。
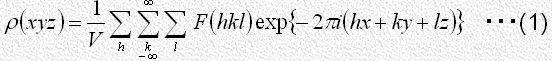
ここで、x, y, z は実際の長さをa, b, c方向の単位格子の長さで割った値[1]。
式(1)は無限級数ですが、実際には収斂性があって適当な項数を用いた次の式
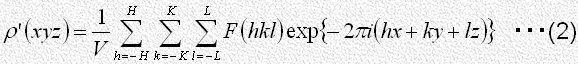
がかなりの近似をもって式(1)を表すことができます。その理由は構造因子
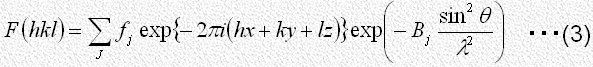
の中で原子構造因子は回折角が大きくなるとともに急速に減速し、それに温度因子が乗ぜられて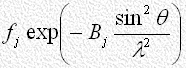 の値はさらに急速に減速します。
の値はさらに急速に減速します。
また、原子座標 にもとづく項は、単位格子内に含まれる独立な原子の数が多いときには、高次の項については互いに相殺する機会が多いため一般に大きな値をとりません。実際に多くの場合実測された反射強度から得られた
にもとづく項は、単位格子内に含まれる独立な原子の数が多いときには、高次の項については互いに相殺する機会が多いため一般に大きな値をとりません。実際に多くの場合実測された反射強度から得られた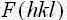 を用いて合成された式(2)がほぼ式(1)に近いことが知られています。これがフーリエ級数法が結晶解析に用いられる第一の理由です。
を用いて合成された式(2)がほぼ式(1)に近いことが知られています。これがフーリエ級数法が結晶解析に用いられる第一の理由です。
フリーデルの法則
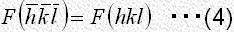
が成立する場合、式(1)は次の形に書くことが出来ます。
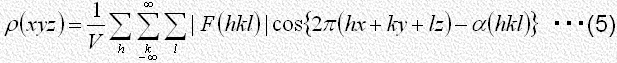
 式(5)の
式(5)の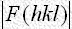 と
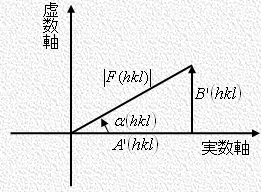
と とは右図に示したように複素構造因子
とは右図に示したように複素構造因子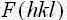 の絶対値と位相角であって、次式によって定められる量です。
の絶対値と位相角であって、次式によって定められる量です。
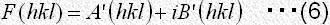
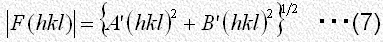
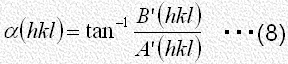
ここで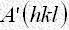 と
と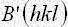 は
は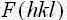 の実数部分と虚数部分であって次式で与えられます。
の実数部分と虚数部分であって次式で与えられます。
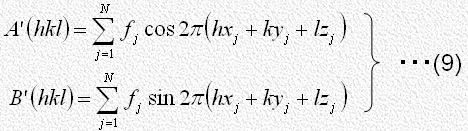
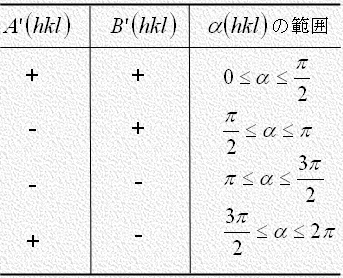 式(8)で与えられる
式(8)で与えられる の値は
の値は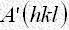 、
、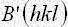 の正負にしたがって表に示される範囲の値をとることに注意して下さい。
の正負にしたがって表に示される範囲の値をとることに注意して下さい。
式(5)に示されるように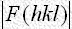 と
と とが既知ならば電子密度
とが既知ならば電子密度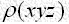 は単にフーリエ級数の和として算出できます。一方
は単にフーリエ級数の和として算出できます。一方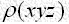 が与えられれば、そこに存在する原子の座標値と原子番号とを推定することが出来ます。
が与えられれば、そこに存在する原子の座標値と原子番号とを推定することが出来ます。
式(5)の係数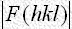 は実験から求められる量ですが、
は実験から求められる量ですが、 を実験的に直接求めることは出来ません[2]。したがって一般には未知構造の結晶について直ちに式(5)の級数を計算することはできません。
を実験的に直接求めることは出来ません[2]。したがって一般には未知構造の結晶について直ちに式(5)の級数を計算することはできません。
ところが、この は、もしも結晶内に含まれる全ての原子の座標
は、もしも結晶内に含まれる全ての原子の座標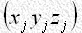 がわかっていれば、式(8)、式(9)によって算出することができる量です。たとえば、既に結晶構造がわかった物質について結晶内電子密度を精密に決定するというような場合はこれに相当します。
がわかっていれば、式(8)、式(9)によって算出することができる量です。たとえば、既に結晶構造がわかった物質について結晶内電子密度を精密に決定するというような場合はこれに相当します。
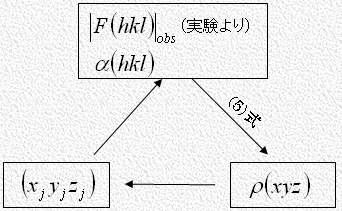 しかし、結晶構造未知の場合には、座標
しかし、結晶構造未知の場合には、座標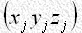 がわかっていないので
がわかっていないので を算出するわけにはいかないという矛盾に陥ります(右図)。この矛盾は結晶構造解析における本質的な困難がフーリエ級数法に表れたものであって、これを解決しようという努力が位相問題です。
を算出するわけにはいかないという矛盾に陥ります(右図)。この矛盾は結晶構造解析における本質的な困難がフーリエ級数法に表れたものであって、これを解決しようという努力が位相問題です。
このような本質的な困難を含むにもかかわらず、フーリエ級数法が結晶解析に広く応用させられているのは、試謬法(しびゅうほう)、パターソン法などで得られた大雑把なモデルから出発して図のサイクルを繰り返し、次第に近似を高めてゆくことが出来るからです。また、何らかの方法で を推定することができれば、式(5)のフーリエ合成を行って、原子の座標
を推定することができれば、式(5)のフーリエ合成を行って、原子の座標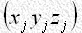 を推定することができるわけであって、不等式法その他の直接位相決定法は主として、この線に沿った工夫です。また結晶の単位格子内に少数の重原子が含まれていて、それらの座標がわかっているときは、それら重原子の寄与で
を推定することができるわけであって、不等式法その他の直接位相決定法は主として、この線に沿った工夫です。また結晶の単位格子内に少数の重原子が含まれていて、それらの座標がわかっているときは、それら重原子の寄与で の近似値が与えられ、近似的な
の近似値が与えられ、近似的な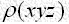 を算出することが出来ます。これについては続いて重原子法のページで説明します。
を算出することが出来ます。これについては続いて重原子法のページで説明します。
重原子法
結晶の構造因子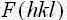 は式(6)、式(9)からわかるように、単位格子内の各原子から散乱される波が合成されたものであるから、X線の散乱に与かる電子を多く含むいわゆる重原子Mが存在すると、結晶の構造因子の位相角
は式(6)、式(9)からわかるように、単位格子内の各原子から散乱される波が合成されたものであるから、X線の散乱に与かる電子を多く含むいわゆる重原子Mが存在すると、結晶の構造因子の位相角 は多くの場合重原子の寄与で近似できることを示します。
は多くの場合重原子の寄与で近似できることを示します。
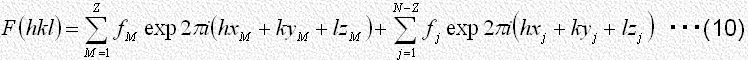
式(10)で右辺の第1項は重原子の寄与をあらわし、第2項は残りの軽原子の寄与をあらわす。
この位相角は次の式で与えられます。
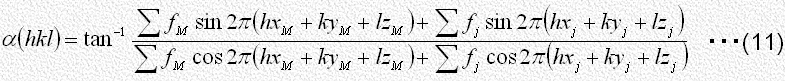
軽原子の単位格子内での分布は比較的一様であると仮定すれば、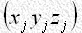 は種々の値をとるので、軽原子の
は種々の値をとるので、軽原子の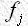 が似た値であるならば、式(11)の分母、分子の第2項は互いに打ち消しあう確率が大きい[3]。他方、Mは重原子であって
が似た値であるならば、式(11)の分母、分子の第2項は互いに打ち消しあう確率が大きい[3]。他方、Mは重原子であって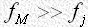 であるとすれば
であるとすれば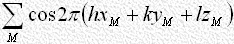 あるいは
あるいは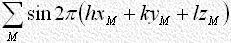 が非常に小さな値とならないかぎり[4]、式(11)の分母、分子の第1項は第2項に比して一般にずっと大きいと考えてよいので、式(11)は近似的に次のようになります。
が非常に小さな値とならないかぎり[4]、式(11)の分母、分子の第1項は第2項に比して一般にずっと大きいと考えてよいので、式(11)は近似的に次のようになります。
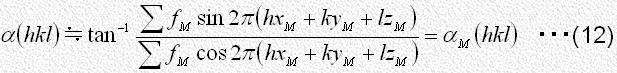
式(12)は結晶全体の位相角 が重原子のみによる位相角
が重原子のみによる位相角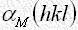 で近似できることを意味していますが、一方重原子の座標値
で近似できることを意味していますが、一方重原子の座標値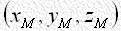 はパターソン法などで容易に決定できるので、その位相角
はパターソン法などで容易に決定できるので、その位相角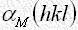 はかなり正確に計算できます。
はかなり正確に計算できます。
この位相角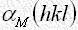 を第一近似として結晶全体の位相角
を第一近似として結晶全体の位相角 の代わりに用い、実測構造因子
の代わりに用い、実測構造因子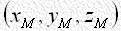 を係数としてフーリエ合成を行うと、得られた
を係数としてフーリエ合成を行うと、得られた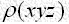 には、重原子のピークはもちろんのこと、軽原子に相当するピークもある程度あらわれるのが普通です。それは実測値
には、重原子のピークはもちろんのこと、軽原子に相当するピークもある程度あらわれるのが普通です。それは実測値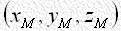 の方には軽原子の寄与が含まれているから、たとえ位相角の方には軽原子の寄与が含まれていなくても、これから算出した
の方には軽原子の寄与が含まれているから、たとえ位相角の方には軽原子の寄与が含まれていなくても、これから算出した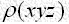 には軽原子に対応するピークが不充分ながらも現れます。
には軽原子に対応するピークが不充分ながらも現れます。
式(11)において実測した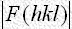 が比較的大きいのに重原子の寄与が分母、分子ともにあまり大きくなく、位相角
が比較的大きいのに重原子の寄与が分母、分子ともにあまり大きくなく、位相角 の近似がひどく悪い見込みのある項は、最初の
の近似がひどく悪い見込みのある項は、最初の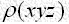 の求和から除く方が安全です。このようにして
の求和から除く方が安全です。このようにして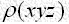 の求和に必要な項の一部を省いたときは、それに起因するいわゆるゴーストのピークが不規則な形で現れ、軽原子をあらわす真のピークと見分けがつかなかったり、軽原子のピークを小さくしたり、ひずませたりするとこがあります。よって、このような不完全な
の求和に必要な項の一部を省いたときは、それに起因するいわゆるゴーストのピークが不規則な形で現れ、軽原子をあらわす真のピークと見分けがつかなかったり、軽原子のピークを小さくしたり、ひずませたりするとこがあります。よって、このような不完全な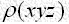 から軽原子の位置を見出すには、それらしい場所に一応軽原子の位置を仮定して構造因子を算出し、その絶対値
から軽原子の位置を見出すには、それらしい場所に一応軽原子の位置を仮定して構造因子を算出し、その絶対値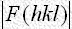 の計算値と実測値との一致が、それら軽原子を加えたことによって、どの程度改善させられるかを検討して決めます。
の計算値と実測値との一致が、それら軽原子を加えたことによって、どの程度改善させられるかを検討して決めます。
結晶に対称心があるとき、またはその投影に対称心があるときには、原点を対称心に一致させれば、 を決めることは単に
を決めることは単に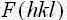 の符号を決めることとなり、問題はそれだけ簡単化します。ただこの場合にも、ある項
の符号を決めることとなり、問題はそれだけ簡単化します。ただこの場合にも、ある項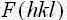 について、もしも間違った符号を採用したとすると、その項を全く省いた場合に比べて2倍の誤差を導入したことになるから、符号の確実でない項はフーリエ合成から除いた方が安全です。
について、もしも間違った符号を採用したとすると、その項を全く省いた場合に比べて2倍の誤差を導入したことになるから、符号の確実でない項はフーリエ合成から除いた方が安全です。
この重元素法を利用してKH2PO4を解いた実例は以下の論文に記されています。
West, J., Z., Krist., 74, 306 (1930)
注釈
[1] 分率座標のことです。
[2] 位相角 を実験的に求める試みは異常分散による方法および電子線回折における同時反射(文献:Kambe, K., Acta Cryst., 7, 777 (1954))による方法が述べられています。
を実験的に求める試みは異常分散による方法および電子線回折における同時反射(文献:Kambe, K., Acta Cryst., 7, 777 (1954))による方法が述べられています。
後者は調べきれていませんが、前者は実際に用いられた例があります。文献:Peerdeman, A.F., Bijvoet. J. M., Raman, S., Z., Krist., 111, 301 (1959)
[3] まれに、偶然に各軽原子からの波がある(hkl)で強め合って大きな値になることもあります。この場合には重原子による近似は成り立ちません。
[4] 実際にはこれらの両方がともに小さいときだけが問題で、どちらか片方が小さくても他方が大きければ位相角は重原子によって支配されることが多い。

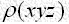 は構造因子
は構造因子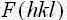 を係数とする次のような三次元フーリエ級数で表すことが出来ます。
を係数とする次のような三次元フーリエ級数で表すことが出来ます。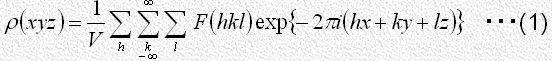
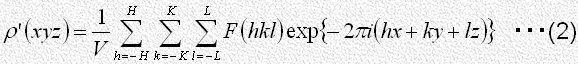
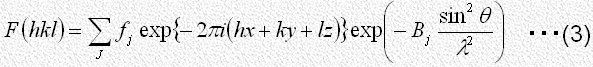
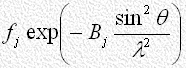 の値はさらに急速に減速します。
の値はさらに急速に減速します。 にもとづく項は、単位格子内に含まれる独立な原子の数が多いときには、高次の項については互いに相殺する機会が多いため一般に大きな値をとりません。実際に多くの場合実測された反射強度から得られた
にもとづく項は、単位格子内に含まれる独立な原子の数が多いときには、高次の項については互いに相殺する機会が多いため一般に大きな値をとりません。実際に多くの場合実測された反射強度から得られた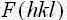 を用いて合成された式(2)がほぼ式(1)に近いことが知られています。これがフーリエ級数法が結晶解析に用いられる第一の理由です。
を用いて合成された式(2)がほぼ式(1)に近いことが知られています。これがフーリエ級数法が結晶解析に用いられる第一の理由です。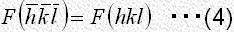
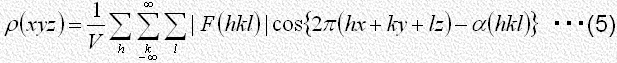
 式(5)の
式(5)の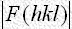 と
と とは右図に示したように複素構造因子
とは右図に示したように複素構造因子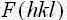 の絶対値と位相角であって、次式によって定められる量です。
の絶対値と位相角であって、次式によって定められる量です。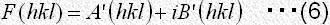
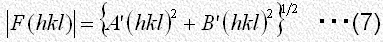
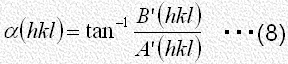
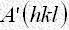 と
と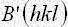 は
は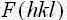 の実数部分と虚数部分であって次式で与えられます。
の実数部分と虚数部分であって次式で与えられます。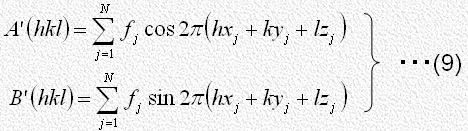
 式(8)で与えられる
式(8)で与えられる の値は
の値は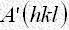 、
、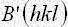 の正負にしたがって表に示される範囲の値をとることに注意して下さい。
の正負にしたがって表に示される範囲の値をとることに注意して下さい。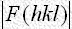 と
と とが既知ならば電子密度
とが既知ならば電子密度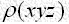 は単にフーリエ級数の和として算出できます。一方
は単にフーリエ級数の和として算出できます。一方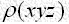 が与えられれば、そこに存在する原子の座標値と原子番号とを推定することが出来ます。
が与えられれば、そこに存在する原子の座標値と原子番号とを推定することが出来ます。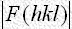 は実験から求められる量ですが、
は実験から求められる量ですが、 を実験的に直接求めることは出来ません[2]。したがって一般には未知構造の結晶について直ちに式(5)の級数を計算することはできません。
を実験的に直接求めることは出来ません[2]。したがって一般には未知構造の結晶について直ちに式(5)の級数を計算することはできません。 は、もしも結晶内に含まれる全ての原子の座標
は、もしも結晶内に含まれる全ての原子の座標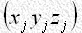 がわかっていれば、式(8)、式(9)によって算出することができる量です。たとえば、既に結晶構造がわかった物質について結晶内電子密度を精密に決定するというような場合はこれに相当します。
がわかっていれば、式(8)、式(9)によって算出することができる量です。たとえば、既に結晶構造がわかった物質について結晶内電子密度を精密に決定するというような場合はこれに相当します。 しかし、結晶構造未知の場合には、座標
しかし、結晶構造未知の場合には、座標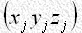 がわかっていないので
がわかっていないので を算出するわけにはいかないという矛盾に陥ります(右図)。この矛盾は結晶構造解析における本質的な困難がフーリエ級数法に表れたものであって、これを解決しようという努力が位相問題です。
を算出するわけにはいかないという矛盾に陥ります(右図)。この矛盾は結晶構造解析における本質的な困難がフーリエ級数法に表れたものであって、これを解決しようという努力が位相問題です。 を推定することができれば、式(5)のフーリエ合成を行って、原子の座標
を推定することができれば、式(5)のフーリエ合成を行って、原子の座標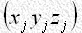 を推定することができるわけであって、不等式法その他の直接位相決定法は主として、この線に沿った工夫です。また結晶の単位格子内に少数の重原子が含まれていて、それらの座標がわかっているときは、それら重原子の寄与で
を推定することができるわけであって、不等式法その他の直接位相決定法は主として、この線に沿った工夫です。また結晶の単位格子内に少数の重原子が含まれていて、それらの座標がわかっているときは、それら重原子の寄与で の近似値が与えられ、近似的な
の近似値が与えられ、近似的な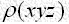 を算出することが出来ます。これについては続いて重原子法のページで説明します。
を算出することが出来ます。これについては続いて重原子法のページで説明します。
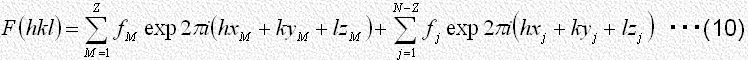
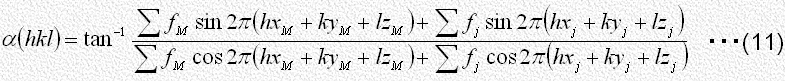
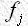 が似た値であるならば、式(11)の分母、分子の第2項は互いに打ち消しあう確率が大きい
が似た値であるならば、式(11)の分母、分子の第2項は互いに打ち消しあう確率が大きい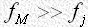 であるとすれば
であるとすれば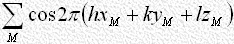 あるいは
あるいは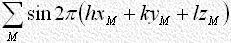 が非常に小さな値とならないかぎり
が非常に小さな値とならないかぎり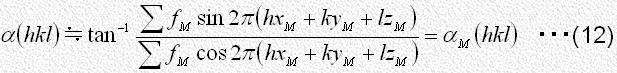
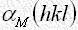 で近似できることを意味していますが、一方重原子の座標値
で近似できることを意味していますが、一方重原子の座標値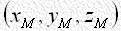 はパターソン法などで容易に決定できるので、その位相角
はパターソン法などで容易に決定できるので、その位相角